Geologia e Python: uno script per le prove penetrometriche

In un post precedente abbiamo parlato di prove penetrometriche con le relative modalità esecutive.

Inoltre abbiamo visto come sia molto utile l’impiego di Python nelle geoscienze. In questo post vediamo come elaborare e creare il grafico di una prova penetrometrica media – dopo la fase di lavoro in campagna – usando Python, nello specifico Pyplot e Pandas.

Prima di iniziare a scrivere il codice dobbiamo preparare un file csv da usare durante l’elaborazione. Dentro un foglio Excell – anche se io uso LibreOffice Calc, un foglio elettronico libero, componente del software di produttività personale LibreOffice – inseriamo le profondità raggiunte con i relativi numeri di colpi. Una volta completato il file lo esportiamo in formato csv.

Il codice Python per il grafico delle prove penetrometriche

Innanzitutto prepariamo l’ambiente di lavoro importando le librerie necessarie.

import pandas as pd 
import matplotlib.pyplot as plt

Adesso importiamo il file csv che contiene i dati, usando pandas, e creiamo due liste: una che contiene le profondità ed una che contiene il numero di colpi.

db= pd.read_csv("dpl.csv", sep=",")

colpi=db.iloc[:,1]
profondita=db.iloc[:,0]

Inseriamo nello script le caratteristiche del penetrometro usato per questa prova penetrometrica (una DPM). Inoltre con un ciclo for compiliamo la lista Rd con i valori di resistenza dinamica alla punta, calcolata con la formula degli olandesi:

Il codice Python per questa parte è:

m=30
M=m**2
H=0.20
sup_punta=10
peso_asta=2.4
altri_pesi=18

P=(peso_asta*4)+altri_pesi

Rd=[]


for N in colpi:
    Rd.append((M*H/(30+P))*N)

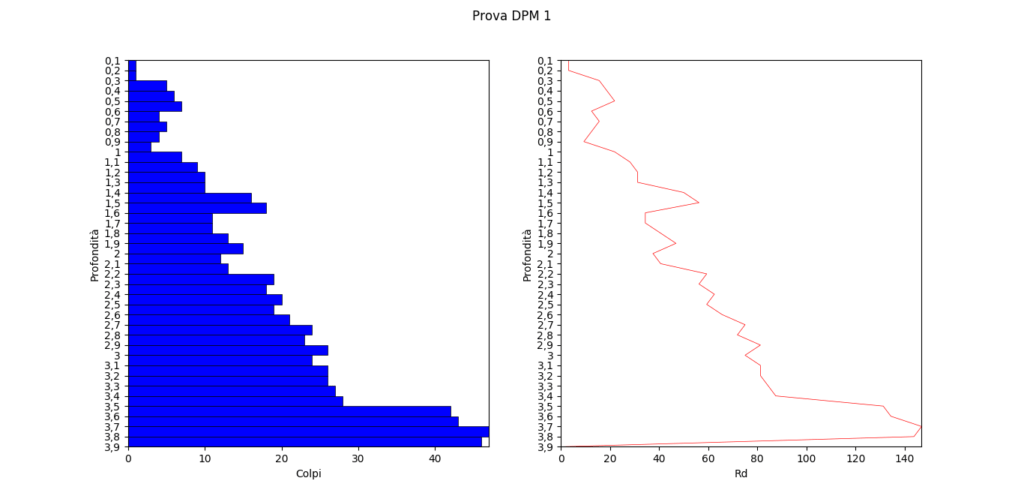
print(Rd)

Procediamo con il codice in modo da creare i grafici delle prove penetrometriche: posizioniamo a sinistra il grafico profondità-numero di colpi mentre a destra il grafico profondità-resistenza alla punta. Usiamo plt.subplot() per affiancare i due grafici.

#grafico profondità-colpi
plt.suptitle('Prova DPM 1')
plt.subplot(121)
plt.barh(profondita, colpi, color= 'blue', align='edge', height=1, edgecolor='black', linewidth=0.5)


plt.xlim(0, 47)
#plt.xticks(range(0,48))
plt.xlabel('Colpi')

# Impostazione dei limiti dell'asse Y

ymin, ymax = min(profondita), max(profondita)
plt.ylim(ymin, ymax)
plt.gca().invert_yaxis()
plt.ylabel('Profondità')

#Grafico resistenza alla punta - profondità

plt.subplot(122)
plt.plot(Rd,profondita, color='red', linewidth=0.5)

# Impostazione dei limiti dell'asse Y

ymin, ymax = min(profondita), max(profondita)
plt.ylim(ymin, ymax)
plt.gca().invert_yaxis()
plt.ylabel('Profondità')

xmin, xmax = min(Rd), max(Rd)
plt.xlim(xmin, xmax)
plt.xlabel('Rd')

plt.show()

Il grafico risultante é

Approfondimenti

Per approfondire l’argomento trattatato in questo post consiglio i seguenti testi: