Perchè Marte è rosso?
23 Ottobre 2018Il geologo, il picco del petrolio e…il genio della lampada!
30 Novembre 2018Uno dei compiti del geologo è eseguire analisi di stabilità dei versanti. Per quanto riguarda i versanti in roccia, ad esempio è fondamentale capire come interagiscono tra loro le varie famiglie di fratture che attraversano l’ammasso roccioso stesso.
Le discontinuità influenzano il modo in cui una roccia reagisce agli stresses, quindi il suo comportamento a rottura che può portare ad una frana del versante in roccia.
In questo post propongo uno script Python per il calcolo del criterio di rottura di Hoek & Brown.

L’indice GSI (Geological Strenght Index)
Un parametro importante per il criterio di rottura di Hoek-Brown è l’indice GSI. La metodologia per la sua stima è spiegata meticolosamente da Hoek et al. (2002), dove vengono descritti un metodo con dati quantitativi e uno con dati qualitativi. In questo post parleremo solo del primo metodo.
GSI da dati quantitativi
I dati da usare vengono prelevati in campagna a sono: Ja e Jr oppure Jcond89 e Jv.
- Ja (numero di alterazione delle fratture): si ricava dalla Tabella 3 dell’articolo;
- Jr (numero di rugosità delle fratture): si ricava dalla Tabella 3 dell’articolo;
- Jcond89 esprime le condizioni delle fratture: si ricava dalla Tabella 1 dell’articolo;
- Jv (conto volumetrico delle fratture). E’ funzione della spaziatura delle discontinuità nell’ammasso roccioso. Da Palmstron abbiamo
:
(1) ![]()
Dove S è lo spazio tra i diversi set di discontinuità.
Per stimare l’indice GSI possono essere usate le seguenti formule:
(2) 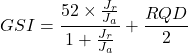
(3) ![]()
nella quale:
(4) ![]()
Il criterio generalizzato di Hoek-Brown
Per il criterio di rottura di Hoek-Brown è necessario determinare, o stimare, per l’ammasso oltre il GSI altri tre parametri di base:
- La resistenza a compressione uniassiale
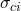 (MPa) degli elementi di roccia intatta, valutata solitamente mediante prove Point Load o assimilate.
(MPa) degli elementi di roccia intatta, valutata solitamente mediante prove Point Load o assimilate. - La costante litologica mi (adimensionale) che dipende dalla litologia dell’ammasso e stimabile da apposite tabelle.
- Il fattore di disturbo D (adimensionale) che variando da 0 a 1 rappresenta il grado di disturbo indotto da operazioni di scavo meccanico o esplosivi.
Tutti questi parametri possono essere stimati usando grafici o tabelle, oltre che misurati direttamente come la resistenza alla compressione uniassiale.
In questo caso un importante ausilio può essere trovato in questo link.
Questo software on-line sostituisce completamente il software ROCKLAB 1.0 (link) che non è più possibile scaricare gratuitamente da internet dato che è stato sostituito da una versione a pagamento (ROCKDATA 5.0).
Il software ORMAS 1.0, invece totalmente freeware, è un importante strumento per la stima dei parametri del metodo partendo da informazioni di campagna e di laboratorio.
Il criterio di rottura generalizzato di Hoek-Brown, analiticamente, è dato da:
(5) ![]()
dove:
(6) ![]()
(7) ![]()
(8) ![]()
Lo sforzo normale e lo sforzo di taglio sono legati agli stress principali dalle seguenti formule:
(9) ![]()
(10) 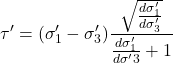
dove:
(11) ![]()
Il criterio di rottura di Hoek-Brown è correlabile al criterio di Mohr-Coulomb attraverso una linea retta di interpolazione di un range che sta nei seguenti limiti:
(12) ![]()
- Limite superiore
- Limite inferiore
Il limite superiore è dato dalla seguente formula:
(13) ![]()
nella quale:
(14) ![]()
(15) ![]()
(16) ![]()
(17) ![]()
Che cosa è Python
Python è un linguaggio di altissimo livello: la sua sintassi, ovvero il modo in cui si scrive, è praticamente identica all’inglese scritto. Questo fa si che rispetto ad altri linguaggi di programmazione come Java e C++, ricordare le varie istruzioni di Python sia estremamente semplice e rapido.
Python può essere impiegato come scelta efficace in ogni applicazione e progetto, sia questo di piccole o grandi dimensioni. Questa sua caratteristica fa si che lo si incontri in qualsiasi scenario di sviluppo software moderno. Lo sapevi che Python è uno dei linguaggi alla base di servizi e siti web estremamente famosi come Instagram, YouTube e Mozilla Firefox?
La velocità di scrittura del codice è uno dei suoi più grandi punti di forza. Nel mondo di Python ogni riga vale davvero, e puoi contare su una libreria composta da oltre 140.000 moduli pronti ad essere installati. È un linguaggio di programmazione pensato per fare, sviluppato per assecondare le esigenze di programmatori e programmatrici!
Approfondimenti
Per approfondire gli argomenti trattati in questo post si consigliano i seguenti testi:
Lo script python
Per iniziare importiamo le librerie necessarie
[python]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
[/python]
Adesso calcoliamo l’indice GSI attraverso le formule descritte in precedenza. I valori usati sono riferiti al Marmo di Carrara.
[python]
plt.style.use(‘seaborn-dark’)
Ja = 2.0
Jr = 2.0
Jv = (1/.15)+(1/.25)+(1/.55)
print(Jv)
RQD = 110 – 2.5 * Jv
print(RQD)
GSI = ((52 * (Jr/Ja)) / (1 + (Jr/Ja))) + (RQD / 2)
print(GSI)
[/python]
Una volta ottenuto l’indice GSI possiamo calcolare il criterio di rottura di Hoek & Brown. I valori usati nelle formule si riferiscono sempre al Marmo di Carrara.
[python]
sigci = 99
mi = 9
D = 1
peso_volume = 0.0265
H = 25
mb = mi * np.exp((GSI-100)/(28-(14*D)))
s = np.exp((GSI-100)/(9-(3*D)))
a = (1/2)+(1/6)*(np.exp(-GSI/15)-np.exp(-20/3))
[/python]
Definiamo una funzione per creare un DataFrame con i calcoli di Hoek.Brown usando un range di valori di σ3. Questa funzione richiederà il limite inferiore, il limite superiore e i numeri da valutare.
Per questi valori la funzione calcolerà σ1, lo stress normale e lo stress di taglio (σn e τ) usando le formule proposte da Hoek-Brown.
[python]
def hoek_brown(min_sig3, max_sig3, num_values):
sig3 = np.linspace(min_sig3, max_sig3, num_values, endpoint=True)
sig1 = sig3 + sigci * ((mb * (sig3/sigci))+s)**a
sig_array = pd.DataFrame(data=np.vstack([sig3, sig1]).T, columns=[‘sig3’, ‘sig1’])
sig_array[‘ds1ds3’] = 1+a*mb*(mb*(sig3/sigci)+s)**(a-1)
sig_array[‘sign’] = ((sig1 + sig3)/2) – ((sig1 – sig3)/2) * (sig_array[‘ds1ds3’] – 1) / (sig_array[‘ds1ds3’] + 1)
sig_array[‘tau’] = (sig1-sig3)*np.sqrt(sig_array[‘ds1ds3’])/(sig_array[‘ds1ds3’]+1)
return sig_array
sig_array = hoek_brown(0, 1, 15)
sig_array.dropna(inplace=True)
print(sig_array)
[/python]
Usando il modulo matplotlib rappresentiamo graficamente l’inviluppo di rottura di Hoek & Brown
[python]
# Plot grafico_1
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(121)
ax.plot(sig_array.sig3.values, sig_array.sig1.values, ‘go-‘,
label=’Hoek-Brown’);
ax.set_xlabel(u’Principal Stress, ![]() , MPa’, fontsize=11)
, MPa’, fontsize=11)
ax.set_ylabel(u’Principal Stress, ![]() , MPa’, fontsize=11)
, MPa’, fontsize=11)
ax.grid(); ax.legend(fontsize=’x-large’)
ax = fig.add_subplot(122)
ax.plot(sig_array[‘sign’], sig_array[‘tau’], ‘go-‘,
label=’Hoek-Brown’)
ax.set_xlabel(u’Normal Stress, ![]() , MPa’, fontsize=11)
, MPa’, fontsize=11)
ax.set_ylabel(u’Shear Stress, ![]() , MPa’, fontsize=11)
, MPa’, fontsize=11)
# Aggiungo i cerchi di Mohr per gli intervalli definiti di seguito:
centers = ((sig_array.sig1.values – sig_array.sig3.values) / 2) \
+ sig_array.sig3.values
radius = sig_array.sig1.values – centers
for r, c in zip(radius, centers):
ax.add_patch(plt.Circle([c, 0], r, facecolor=’none’, ec=’k’, alpha=.2))
ax.grid()
ax.set_aspect(‘equal’)
ax.legend(fontsize=’large’)
fig.suptitle(‘Criterio di rottura di Hoek & Borwn’, fontsize=11, y=1.05)
fig.tight_layout(pad=1.5)
fig.savefig(‘grafico_1.png’, dpi=200)
[/python]
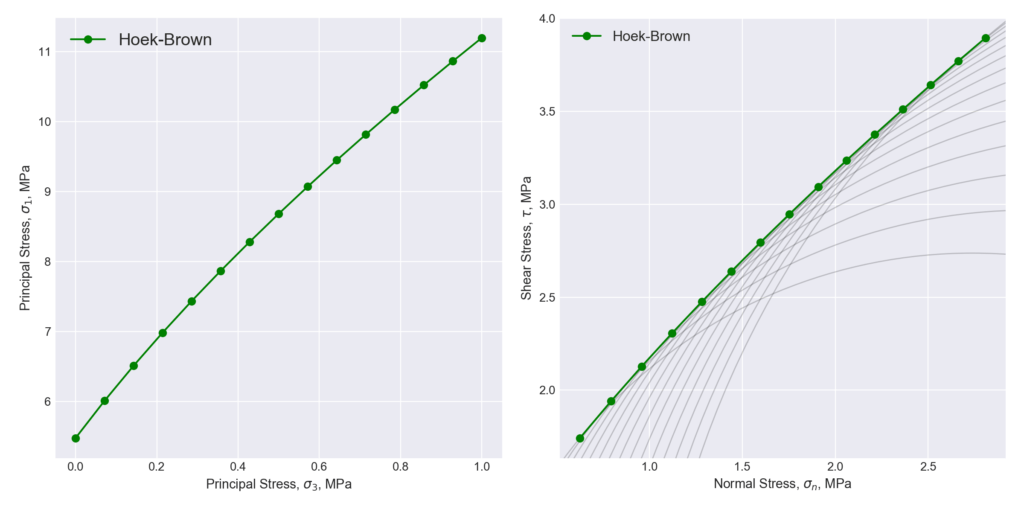
Adesso scriviamo la porzione di codice per il calcolo del criterio di rottura di Mohr-Coulomb:
[python]
#AGGIUNTA DEL CRITERIO DI MOHR-COULOMB
#Valore minimo
sigcm = sigci * (mb+4*s-a*(mb-8*s))*\
(((mb/4)+s)**(a-1))/(2*(1+a)*(2+a))
sigt = -s*sigci/mb
#Valore massimo
sig3_max = sigcm * 0.72 *\
(sigcm / (peso_volume * H))**(-.91)
sig_array_relat = hoek_brown(sigt, sig3_max, 99)
sig_array_relat.dropna(inplace=True)
[/python]
Con il modulo sklearn creo la linea di interpolazione fra i due criteri di rottura.
[python]
#Uso sklearn per fittare una funzione linear in questo intervallo per trovare il criterio di rottura di Mohr-Coulomb:
from sklearn.linear_model import LinearRegression
# Definisco un modello di regressione lineare
lr = LinearRegression()
# Plotto una linea passante per gli stresses principali
lr.fit(sig_array_relat.sig3.values.reshape(-1, 1), \
sig_array_relat.sig1.values.reshape(-1, 1))
# Produzione dei valori
sig1_mohr = lr.predict(sig_array_relat.sig3.values.reshape(-1, 1))\
.ravel()
# Calcolo l’angolo di attrito
k = lr.coef_.squeeze()
phi = np.abs(np.rad2deg(np.arcsin((1 – k)/(1 + k))))
# Plotto un’altra linea usando lo stress normale e lo stress di taglio
lr.fit(sig_array_relat[‘sign’].values.reshape(-1, 1), sig_array_relat[‘tau’].values.reshape(-1, 1))
# Produzione dei valori
tau_mohr = lr.predict(sig_array_relat[‘sign’].values.reshape(-1, 1)).ravel()
# Calcolo la coesione
coh = lr.predict(0).squeeze()
[/python]
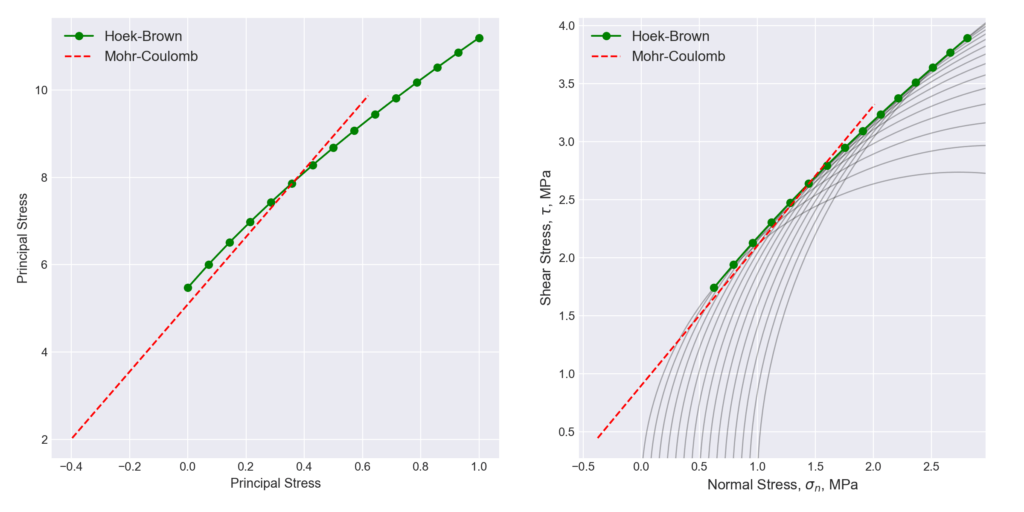
A questo punto non ci resta che plottare il grafico finale:
[python]
# Plot grafico_2
plt.style.use(‘seaborn-dark’)
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(121)
ax.plot(sig_array.sig3.values, sig_array.sig1.values, ‘go-‘, label=’Hoek-Brown’);
ax.plot(sig_array_relat.sig3.values, sig1_mohr, ‘r–‘, label=’Mohr-Coulomb’)
ax.set_xlabel(u’Principal Stress’, fontsize=11)
ax.set_ylabel(u’Principal Stress’, fontsize=11)
ax.grid(); ax.legend(fontsize=’large’)
ax = fig.add_subplot(122)
ax.plot(sig_array[‘sign’], sig_array[‘tau’],
‘go-‘, label=’Hoek-Brown’)
ax.plot(sig_array_relat[‘sign’], tau_mohr,
‘r–‘, label=’Mohr-Coulomb’)
ax.set_xlabel(u’Normal Stress, ![]() , MPa’, fontsize=12)
, MPa’, fontsize=12)
ax.set_ylabel(u’Shear Stress, ![]() , MPa’, fontsize=12)
, MPa’, fontsize=12)
centers = ((sig_array.sig1.values – sig_array.sig3.values) / 2) + sig_array.sig3.values
radius = sig_array.sig1.values – centers
for r, c in zip(radius, centers):
ax.add_patch(plt.Circle([c, 0], r, facecolor=’none’, ec=’k’, alpha=.3))
ax.grid()
ax.set_aspect(‘equal’)
ax.legend(fontsize=’large’)
fig.suptitle(‘Criterio di rottura di Hoek-Brown’, fontsize=20, y=1.05)
fig.tight_layout(pad=1.5)
fig.savefig(‘grafico_2’, dpi=200)
#Risultati
sigtm = 0.5*sigci*(mb-np.sqrt((mb**2)+4*s))
Em = (1 – (D/2)) * (np.sqrt(sigci/100.0)*10**((GSI-10)/40.0)) * 10**3
[/python]
Importando la libreria ReportLab possiamo esportare alcuni risultati su un documento pdf. Trovo questa libreria molto utile, ad esempio per la stesura di report da inserire nelle nostre relazioni geologiche.
[python]
#from reportlab.pdfgen import canvas
c = canvas.Canvas("Report.pdf")
c.drawString(100,750,"GSI: %s"%GSI)
c.drawString(100,765,"c’: %s"%coh)
c.drawString(100,780,"phi’: %s"%round(phi,2)
c.drawString(100,735,"RQD: %s"%RQD)
c.save()
[/python]
